攻击条件：

当Alice使用同一公钥对两个具有线性关系的信息M1与M2进行加密，并将加密后的信息c1,c2发送给了Bob，我们就可能可以获得对应的信息M1与M2。这里我们假设模数为N，两者之间的线性关系如下：
$$
M_1 ≡ f(M_2)\ mod\ N
$$
其中f为一个线性函数，比如：f = ax+b

在具有较小错误概率的情况下，其复杂度为O(elog^2^N)

攻击原理：

$$
\begin{flalign}
&首先，我们知道C_1≡M_1^e\ mod\ N，并且M_1≡f(M_2)\ mod\ N，\
&那么我们可以知道M_2是f(x)^e≡C_1\ mod\ N的一个解，\
&即它是方程f(x)^e-C_1在模N意义下的一个根。\
&同样的，M_2是x^e-C_2在模N意义下的一个根。\
&所以说x-M_2同时整除以上两个多项式。\
&因此，我们可以求得两个多项式的最大公因子，如果最大公因子恰好是线性的话，那么我们就求得了M_2\
&需要注意的是，在e=3的情况下，最大公因子一定是线性的

\end{flalign}
$$

  • 既然最后解的形式是**（x-M）**这样的，那么最后只要提结果后面的M即可，这里用sage中的Q.coefficients()[0]

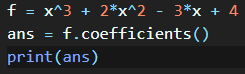
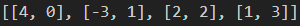
image-20241008205034280image-20241008205055267

最后添加个负号即可得到M

例题：

题目一：

题面：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from secret import flag
from Crypto.Util.number import *

m1 = bytes_to_long(flag)
N = getPrime(512)*getPrime(512)
e = 17

c1 = pow(m1, e, N)

a = getRandomNBitInteger(512)
b = getRandomNBitInteger(512)
m2 = a * m1 + b
c2 = pow(m2, e, N)

print(N, a, b, c1, c2, sep="\n")

# 51296885372346449295388453471330409021784141081351581975478435681552082076338697136130122011636685327781785488670769096434920591920054441921039812310126089859349902066456998315283909435249794317277620588552441456327265553018986591779396701680997794937951231970194353001576159809798153970829987274504038146741
# 13256631249970000274738888132534852767685499642889351632072622194777502848070957827974250425805779856662241409663031192870528911932663995606616763982320967
# 12614470377409090738391280373352373943201882741276992121990944593827605866548572392808272414120477304486154096358852845785437999246453926812759725932442170
# 18617698095122597355752178584860764221736156139844401400942959000560180868595058572264330257490645079792321778926462300410653970722619332098601515399526245808718518153518824404167374361098424325296872587362792839831578589407441739040578339310283844080111189381106274103089079702496168766831316853664552253142
# 14091361528414093900688440242152327115109256507133728799758289918462970724109343410464537203689727409590796472177295835710571700501895484300979622506298961999001641059179449655629481072402234965831697915939034769804437452528921599125823412464950939837343822566667533463393026895985173157447434429906021792720

题解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
n = 51296885372346449295388453471330409021784141081351581975478435681552082076338697136130122011636685327781785488670769096434920591920054441921039812310126089859349902066456998315283909435249794317277620588552441456327265553018986591779396701680997794937951231970194353001576159809798153970829987274504038146741
a = 13256631249970000274738888132534852767685499642889351632072622194777502848070957827974250425805779856662241409663031192870528911932663995606616763982320967
b = 12614470377409090738391280373352373943201882741276992121990944593827605866548572392808272414120477304486154096358852845785437999246453926812759725932442170
c1 = 18617698095122597355752178584860764221736156139844401400942959000560180868595058572264330257490645079792321778926462300410653970722619332098601515399526245808718518153518824404167374361098424325296872587362792839831578589407441739040578339310283844080111189381106274103089079702496168766831316853664552253142
c2 = 14091361528414093900688440242152327115109256507133728799758289918462970724109343410464537203689727409590796472177295835710571700501895484300979622506298961999001641059179449655629481072402234965831697915939034769804437452528921599125823412464950939837343822566667533463393026895985173157447434429906021792720
e = 17

def franklinReiter(n,e,c1,c2,a,b):
	PR.<x> = PolynomialRing(Zmod(n))
    f1 = x^e - c1
    f2 = (a*x+b)^e - c2
    
    def gcd(f1,f2):
        while f2:
            f1 , f2 = f2 , f1 % f2
		return f1.monic()
   	return -gcd(f1,f2)[0]
m=franklinReiter(n,e,c1,c2,a,b)
print(libnum.n2s(int(m)))