Categories
Tags
1249 words
6 minutes
2024 国城杯
babyRSA
题面:
from Crypto.Util.number import*
from gmpy2 import*
def gen_key(p, q):
public_key = p*p*q
e = public_key
n = p*q
phi_n = (p-1)*(q-1)
private_key = inverse(e,phi_n)
return public_key,private_key,e
p = getPrime(512)
q = getPrime(512)
N,d,e = gen_key(p,q)
c = gmpy2.powmod(bytes_to_long(flag),e,N)
print(N)
print(d)
print(c)
'''
N = 539403894871945779827202174061302970341082455928364137444962844359039924160163196863639732747261316352083923762760392277536591121706270680734175544093484423564223679628430671167864783270170316881238613070741410367403388936640139281272357761773388084534717028640788227350254140821128908338938211038299089224967666902522698905762169859839320277939509727532793553875254243396522340305880944219886874086251872580220405893975158782585205038779055706441633392356197489
d = 58169755386408729394668831947856757060407423126014928705447058468355548861569452522734305188388017764321018770435192767746145932739423507387500606563617116764196418533748380893094448060562081543927295828007016873588530479985728135015510171217414380395169021607415979109815455365309760152218352878885075237009
c = 82363935080688828403687816407414245190197520763274791336321809938555352729292372511750720874636733170318783864904860402219217916275532026726988967173244517058861515301795651235356589935260088896862597321759820481288634232602161279508285376396160040216717452399727353343286840178630019331762024227868572613111538565515895048015318352044475799556833174329418774012639769680007774968870455333386419199820213165698948819857171366903857477182306178673924861370469175
'''分析:
Schmidt-Samoa密码体系
给出如下证明:
解密完成
题解:
from Crypto.Util.number import *
pubkey = 539403894871945779827202174061302970341082455928364137444962844359039924160163196863639732747261316352083923762760392277536591121706270680734175544093484423564223679628430671167864783270170316881238613070741410367403388936640139281272357761773388084534717028640788227350254140821128908338938211038299089224967666902522698905762169859839320277939509727532793553875254243396522340305880944219886874086251872580220405893975158782585205038779055706441633392356197489
privkey = 58169755386408729394668831947856757060407423126014928705447058468355548861569452522734305188388017764321018770435192767746145932739423507387500606563617116764196418533748380893094448060562081543927295828007016873588530479985728135015510171217414380395169021607415979109815455365309760152218352878885075237009
enc = 82363935080688828403687816407414245190197520763274791336321809938555352729292372511750720874636733170318783864904860402219217916275532026726988967173244517058861515301795651235356589935260088896862597321759820481288634232602161279508285376396160040216717452399727353343286840178630019331762024227868572613111538565515895048015318352044475799556833174329418774012639769680007774968870455333386419199820213165698948819857171366903857477182306178673924861370469175
pq = gcd(pow(2,pubkey*privkey,pubkey)-2, pubkey)
m = pow(enc, privkey, pq)
print(long_to_bytes(m))Curve
题面:
#sagemath
from Crypto.Util.number import *
def add(P, Q):
(x1, y1) = P
(x2, y2) = Q
x3 = (x1*y2 + y1*x2) * inverse(1 + d*x1*x2*y1*y2, p) % p
y3 = (y1*y2 - a*x1*x2) * inverse(1 - d*x1*x2*y1*y2, p) % p
return (x3, y3)
def mul(x, P):
Q = (0, 1)
while x > 0:
if x % 2 == 1:
Q = add(Q, P)
P = add(P, P)
x = x >> 1
return Q
p = 64141017538026690847507665744072764126523219720088055136531450296140542176327
a = 362
d = 7
e=0x10001
gx=bytes_to_long(b'D0g3xGC{*****************}')
PR.<y>=PolynomialRing(Zmod(p))
f=(d*gx^2-1)*y^2+(1-a*gx^2)
gy=int(f.roots()[0][0])
assert (a*gx^2+gy^2)%p==(1+d*gx^2*gy^2)%p
G=(gx,gy)
eG = mul(e, G)
print(eG)
#eG = (34120664973166619886120801966861368419497948422807175421202190709822232354059, 11301243831592615312624457443883283529467532390028216735072818875052648928463)分析:
assert (a*gx^2+gy^2)%p==(1+d*gx^2*gy^2)%p此处直接标明了曲线的形式:
可以知道为Twisted_Edwards_Curves
现在已知Edcurve上的一个e倍点,求解该e倍点对应的原点G的横坐标,即为flag
假设这是一条常见的椭圆曲线,求解的步骤如下:
用sage的order()函数求解出该椭圆曲线的阶n
求出e关于阶n的逆元,记为t
求倍点G=t*(eG),横坐标即为所求
该求解过程对于Edcurve也是类似的,不过sage不能直接求出Edcurve这种形式的曲线的阶,于是就有了求解思路:
- 将Edcurve通过换元映射,变换为常见的椭圆曲线的形式
- 求解出对应的椭圆曲线的阶,记为s
- 求倍点G^’^ = s*(eG^’^)
- 将求解出的G^‘^再变换回Edcurve上得到G,其横坐标即为所需要的
step1:转换为 Montgomery曲线

step2:Montgomery转换为Weierstrass
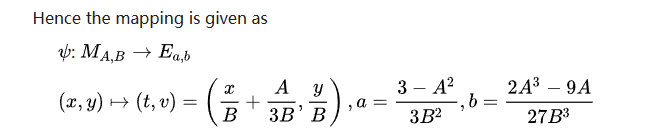
然后求该曲线的阶,从而求解出远原点G,并且重新逆变换回Edcurve,得到的横坐标即为flag
题解:
from Crypto.Util.number import *
eG = (34120664973166619886120801966861368419497948422807175421202190709822232354059, 11301243831592615312624457443883283529467532390028216735072818875052648928463)
p = 64141017538026690847507665744072764126523219720088055136531450296140542176327
a = 362
d = 7
e = 0x10001
c = 1
F = GF(p)
B = F(4)/F(a-d)
A = F(2)*F(a+d)/F(a-d)
def edwards_to_ECC(x,y):
x1 = F(x)/F(1)
y1 = F(y)/F(1)
# now curve is a*x^2 + y^2 = 1 + d*x^2*y^2
x2 = F(1+y1)/F(1-y1)
y2 = F(x2)/F(x1)
# now curve is By^2 = x^3 + Ax^2 + x
x3 = (F(3*x2)+F(A))/F(3*B)
y3 = F(y2)/F(B)
# now curve is y^2 = x^3 + ax + b
return (x3,y3)
def ECC_to_edwards(x3,y3):
x2 = (F(x3)*F(3*B)-F(A))/F(3)
y2 = F(y3)*F(B)
# now curve is By^2 = x^3 + Ax^2 + x
x1 = F(x2)/F(y2)
y1 = F(1)-(F(2)/F(x2+1))
# now curve is a*x^2 + y^2 = 1 + d*x^2*y^2
return (x1,y1)
a = F(3-A^2)/F(3*B^2)
b = F(2*A^3-9*A)/F(27*B^3)
E = EllipticCurve(GF(p), [a, b])
order = E.order()
eG = E(edwards_to_ECC(eG[0],eG[1]))
t = inverse(e,order)
G = t*eG
G = ECC_to_edwards(G[0],G[1])
print(long_to_bytes(int(G[0])))EZ_sign
题面:
from Crypto.Util.number import *
from gmpy2 import *
from hashlib import*
import random,os
flag = b'D0g3xGA{***************}'
msg = b'e = ?'
def sign(pub, pri, k):
(p,q,g,y) = pub
x = pri
r = int(powmod(g, k, p) % q)
H = bytes_to_long(sha1(os.urandom(20)).digest())
s = int((H + r * x) * invert(k, q) % q)
return (H,r,s)
k1 = getPrime(64)
k2 = k1 ** 2
pri = bytes_to_long(msg)
a = 149328490045436942604988875802116489621328828898285420947715311349436861817490291824444921097051302371708542907256342876547658101870212721747647670430302669064864905380294108258544172347364992433926644937979367545128905469215614628012983692577094048505556341118385280805187867314256525730071844236934151633203
b = 829396411171540475587755762866203184101195238207
g = 87036604306839610565326489540582721363203007549199721259441400754982765368067012246281187432501490614633302696667034188357108387643921907247964850741525797183732941221335215366182266284004953589251764575162228404140768536534167491117433689878845912406615227673100755350290475167413701005196853054828541680397
y = 97644672217092534422903769459190836176879315123054001151977789291649564201120414036287557280431608390741595834467632108397663276781265601024889217654490419259208919898180195586714790127650244788782155032615116944102113736041131315531765220891253274685646444667344472175149252120261958868249193192444916098238
pub = (a, b, g, y)
H1, r1, s1 = sign(pub, pri, k1)
H2, r2, s2 = sign(pub, pri, k2)
p = getPrime(128)
q = getPrime(128)
n = p * q
c = powmod(bytes_to_long(flag), e, n)
C = p**2 + q**2
print(f'(H1, r1, s1) = {H1}, {r1}, {s1}')
print(f'(H2, r2, s2) = {H2}, {r2}, {s2}')
print(c)
print(C)
'''
(H1, r1, s1) = 659787401883545685817457221852854226644541324571, 334878452864978819061930997065061937449464345411, 282119793273156214497433603026823910474682900640
(H2, r2, s2) = 156467414524100313878421798396433081456201599833, 584114556699509111695337565541829205336940360354, 827371522240921066790477048569787834877112159142
c = 18947793008364154366082991046877977562448549186943043756326365751169362247521
C = 179093209181929149953346613617854206675976823277412565868079070299728290913658
'''分析:
首先要从线性k的DSA签名中得到x,也就是e
然后coppersmith求出小根k,然后正常解密得到x,也就有了e
接下来对于
直接用sage的two_squares()得到的并不是我们需要的根
看了其他师傅的wp知道了Generic two integer variable equation solver

逐个验证,发现是
p=302951519846417861008714825074296492447
q=295488723650623654106370451762393175957题解:
from Crypto.Util.number import *
from gmpy2 import invert
a = 149328490045436942604988875802116489621328828898285420947715311349436861817490291824444921097051302371708542907256342876547658101870212721747647670430302669064864905380294108258544172347364992433926644937979367545128905469215614628012983692577094048505556341118385280805187867314256525730071844236934151633203
b = 829396411171540475587755762866203184101195238207
g = 87036604306839610565326489540582721363203007549199721259441400754982765368067012246281187432501490614633302696667034188357108387643921907247964850741525797183732941221335215366182266284004953589251764575162228404140768536534167491117433689878845912406615227673100755350290475167413701005196853054828541680397
y = 97644672217092534422903769459190836176879315123054001151977789291649564201120414036287557280431608390741595834467632108397663276781265601024889217654490419259208919898180195586714790127650244788782155032615116944102113736041131315531765220891253274685646444667344472175149252120261958868249193192444916098238
H1, r1, s1 = 659787401883545685817457221852854226644541324571, 334878452864978819061930997065061937449464345411, 282119793273156214497433603026823910474682900640
H2, r2, s2 = 156467414524100313878421798396433081456201599833, 584114556699509111695337565541829205336940360354, 827371522240921066790477048569787834877112159142
c = 18947793008364154366082991046877977562448549186943043756326365751169362247521
C = 179093209181929149953346613617854206675976823277412565868079070299728290913658
p,q = two_squares(C)
print(p,q)
x = (H1*r2-H2*r1) % b
PR.<k> = PolynomialRing(Zmod(b))
f = s1*r2*k - s2*r1*k^2 - x
f = f.monic()
k = int(f.small_roots(X = 2^64,beta = 0.4,epsilon = 0.01)[0])
print(long_to_bytes(int(((s1*k-H1)*invert(r1,b))%b)))
e = 44519
d = invert(e,(p-1)*(q-1))
print(long_to_bytes(pow(c,d,p*q)))